To the Primary Formation of Numerals in the Nostratic Languages
The multidimensionality of quantitative characteristics of the real world has determined the diversity of methods and means of representing the semantic meaning of quantity, forming a functional-semantic field (STEPANOVA. 2007: 1). Such uncertainty, which has been preserved in many languages of the world to this day, should have been limited by the emergence in the language of a special category that allows for a more precise assessment of relationships between objects.
The establishment of such a category in human development represents the beginning of a special form of thinking and its reflection in language. The emergence of numbers and the awareness of the relationships between them determine the nature of the further existence of mental activity. For the mind of primitive man, this feature was a great mystery, and the numbers were attributed to a divine origin. Even rationally thinking people were sure that numbers were important and influenced human life. For people, numbers express numerical relationships and a qualitative connection between themselves. An example is the teaching of Pythagoras, which influenced the further development of the emerging science, for which numbers were not only a tool but an incentive to search for new ideas. Even the author of the theory of relativity, Albert Einstein, recognized the influence of Pythagoras on the development of his thoughts.
However, despite the importance of counting in human intellectual life, there is no known theory of the origin of numerals as a morphological category. Such a theory could provide an answer to the eternal questions of philosophy. To do this, one does not need to delve into details but rather focus on studying the general patterns of counting development using the example of individual languages:
A valuable subject for comparative studies on a larger scale is the individual number systems, the various methods by which the individual languages have arranged the multitude of individual number words into a systematic whole. Despite all the differences in detail, there are nevertheless large, far-reaching lines of commonalities that make it seem promising to examine them for connections with large cultural groups, the cultural circles. This is all the more so because it is precisely here that it is clear that in these large, far-reaching lines, a historical succession of stages of development somehow confronts us. (SCHMIDT ILHELM. 1926: 357—358, quoted after HONTI LÁSZLÓ. 1993: 5 ).
The general pattern of lexical complexes of nominations of quantity is the tiered structure presented in the figure below:
Fig. 1. General structure of sets of quantity nominations
(KOBYAKOVA I.K., SHVACHKO S.A. 2017: 91)
Understanding the concept of numbers and numerals is one of the indicators of the social, economic, and cultural level of a society. The deeper the members of a society penetrated the secrets of counting, the more successful its development was:
Without the exact determination of different quantities, the use of numbers, and their naming, it is hardly conceivable, for example, to plan a group hunt, to cultivate agriculture, and to breed livestock, no matter how primitive this knowledge may be. (HONTI LÁSZLÓ. 1993, 19)
In reconstructing the development of counting and numbers, the starting point should have been an explanation of the origin of cardinal numerals, beginning with the lowest. Numerals form one of the most abstract layers of vocabulary and their meaning is the most stable and least subject to semantic changes (Ibid: 21). However, a comparison of the meaning of phonetically similar numerals shows that this was not the case in the early stages of the development of counting. It has also been noted that "numerals up to 'three' are unmotivated forms" (VINTER V.1989: 37). It is obvious that we should begin with the idea of motivation for the formation of numerals. Etymological research shows that numerals go back to the names of body parts, mainly fingers and toes:
Remnants of dual and triple grammatical numbers, symbols of numbers reminiscent of the position of fingers when counting, and, finally, children's experience of counting (using fingers, nearby objects) are witnesses to the diachronic memory of calculation and measurement (KOBYAKOVA I.K., SHVACHKO S.A. 2017: 97-98).
This is a good point, but the connection between numerals and the human organism and psychology is not limited to this; another idea arose during research into the Nostratic languages and is developed here in the following narration.
In our research, we include Indo-European, Finno-Ugric, Turkic, Semito-Hamitic (Afro-Asiatic), Kartvelian, and Dravidian languages in the Nostratic macrofamily. Many linguists are very cautious about the very existence of such a macrofamily or its composition. The graphic-analytical method, by which their ancestral homeland and the migration routes of the ancient speakers of these languages were determined, remains little known or unperceived. The corresponding map explaining the existence of contacts between the Nostratic languages and their neighbors in different eras, which will be discussed, is given below.
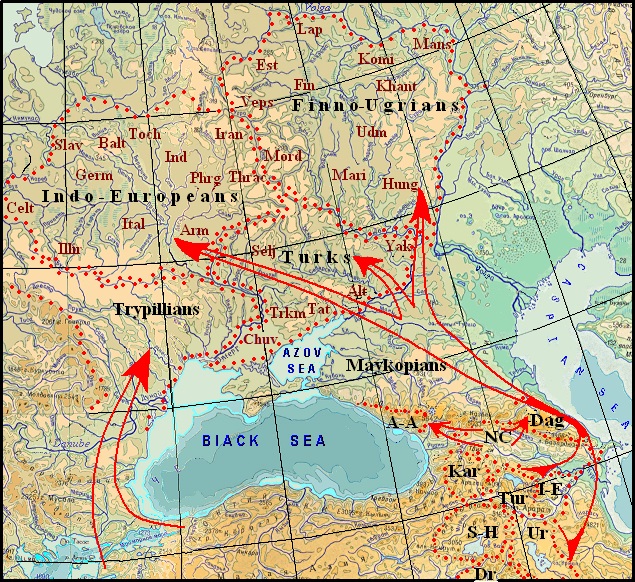 |
The Resettlement of the Indo-European, Turkic, and Finno-Ugric tribes in Eastern Europe.
Legend: Nostratic peoples: A-A – Abkhazo-Adyge, Dag – Dagestanis, Dr – Dravidians, Kar – Kartvelians, I-E – Indo-Europeans, NC – the speakers of North Caucasian language, S/H – Semits-Hamits, Trk – Türks, Ur – Uralians.
Indo-European peoples: Arm – Armenians, Balt – Balts, Gr – Greeks, Germ – Germanic, Illyrians, Ind – Indo-Aryans, Ir – Iranians, Ital – Italics, Celt – Celtic, Slav – Slavs, Toch – Tocharians, Thrac – Thracians, Phrig Phrygians.
Finno-Ugric peoples: Est – Estonians, Fin -Finns, Hung -Hungarians, Khant – Khanty, Lap – Sami, Mans – Mansi, Mord – Mordvinians, Udm – Udmurts.
Turkic peoples: Alt – South Altaians, Chuv – Proto-Chuvashes, Yak – Yakuts, Khak – Khakasians, Tat – Tatars, Trkm -Turkmens.
However, it is possible that other languages, primarily North Caucasian (Abkhaz-Adyghe and Nakh-Dagestan), are also Nostratic. It should be noted that of the so-called "Altaic" languages, we only classify Turkic as Nostratic. In addition, the full lack of similarity between Turkic and Mongolian numerals, not to mention such similarity with Tungus-Manchu, Korean, and Japanese, speaks against the genetic relationship of Turkic and other Altaic languages. (see Table 1).
Table 1. The cardinal numbers of the ancient Turkic and the Mongolian languages.
| one | two | three | four | five | six | seven | eight | nine | ten | |
| Turkic | bir | ikki | üč | tört | beš | alty | jetti | sekiz | toquz | on |
| Mong. | negen | xojor | gurvan | dorvan | tavun | zurgaan | doloon | najman | jisun | arvan |
The importance of the similarity of numerals as an argument for genetic relationship between languages is confirmed by the semblance of numerals within particular language families of the Nostratic phylum, and among the Turkic languages especially. Moreover, some similarities in numerals can also be found among the languages of different Nostratic families. For ease of comparison of numerals up to ten of the particular Nostratic languages, they are summarized in Table 2. The Ingush and Kabardian numerals are assessed too for the estimation of their possible membership to the Nostratic languages.
Table 2. The cardinal numbers of the Nostratic languages.
| English | one | two | three | four | five | six | seven | eight | nine | ten |
| I.-E. | *dvou | *treis | *quetwor | *penque | *seks | *septm | *octou | *newn | *deќm | |
| English | one | two | three | vour | five | six | seven | eight | nine | ten |
| Latin | ūnus | dǔo | trēs | quat-tuor | quīnque | sěx | sěptem | ŏcto | nŏvem | děcěm |
| Armen. | mēk | ērku | ērēk' | č'ors | hing | vēç | yot' | ut' | imê | tasě |
| Anc. Ind | éka | dva | trayas | catv-ara | pañca | shash | sapta | ashtau | nava | dasa |
| Turkic | bir | ikki | üč | tört | beš | alty | jetty | sekiz | toquz | on |
| Chuvash | pěr | ikĕ | viç | tăvattă | pillĕk | ultă | çiče | sakkăr | tăxxăr | vun |
| Finnish | yksi | kaksi | kolme | neljä | viisi | kuusi | seitse-män | kah-deksan | yh-deksän | kymmenen |
| Veps | üks’ | kaks’ | koume | nel’l’ | viž | kuz’ | seič-eme | kahesa | ühesa | kümne |
| Komi | öti | kyk | kuim | väl | vit | kvajt | sizim | kök’ja-mys | ökmys | das |
| Udmurt | kož, ogez | kyk | kuin’ | njil | vit’ | kuat’ | siz’im | t’amys | ukmys | das |
| Erzia | vejke | kavto | kolmo | nile | vete | koto | sisem | kavkso | vejkse | kemen’ |
| Mari | ik | kok | kum | nyl | vič | kud | šym | kandaš | indeš | lu |
| Hung | egy | kettő | három | négy | öt | hat | hét | nyolc | kilenc | tiz |
| Khanty | əj, it | kät | kolem | n’ələ, | wet | kut | tapet | näileg | arjaŋ | jöŋ |
| Mansi | akv | kit | xurum | nila | at | xot | sat | n’ololov | ontolov | lov |
| Georg. | erti | ori | sami | ot’xi | xuti | ekivsi | švidi | rva | cxra | ati |
| Hebrew | axat | šnaim | šaloš | arba | xameš | šeš | ševa’ | šmone | teša, | ‘eser |
| Arab | wāhid | ithnān | thalā-thah | 'arba-ah | xamsah | sittah | sab`ah | thamāniyyah | tis`ah | `ašarah |
| Tamil | onru | eran, ndu | moon-rru | naan-ku | i:ynthu | aarru | aezhu | āddu | onpathu | patthu |
| Telugu | okati | rendu | muudu | naa-lugu | aydu | aaru | eedu | enimidi | tommidi | padi |
| Tulu | onji | radd | mūji | nāl | ein | āji | ēl | enma | ormba | patt |
| Gongi | undi: | rend | mūnd | nā-lūng | siyāng | sārūng | ērūng | armur | anma | putth |
| Malaiali | onnu | rantu | mū-nnu | nālu | ancu | āru | ēlu | ettu | onpatu | pattu |
| Kabard | zy | t’u | ščy | pl’y | txu | xy | b’y | i | bgu | pščy |
| Ingush | ča' | šij | kxo’ | di’ | pxi’ | jalx | vorh | barh | ijs | itt |
Careful examination of the table makes it possible to detect some patterns that can be a starting point for finding the logic of the formation of numerals in the Nostratic languages:
1. Turkic ikki “two” may correspond to some words of Finno-Ugric languages meaning "one" (Erzia vejke, Mari ik, Hung egy, Fin. yksi, Veps. üks'). They have also matches in some Indo-European languages such as O.I. éka “one” and many words of Iranian (Farsi, Tadjic, Kurdish jak, Baluchi, Gilani jek, etc). Maybe Udm odez, Ivrit axat, Ar wāhid, and Telugu okati “one” can be added here too.
2. Some Indo-European and Dravidian languages have similar words for the number one: Lat ūnus, (Gr οινοσ), Ger ein, etc – Tulu onji, Tamil onru, Malayalam onnu, etc.
3. There is some similarity in even numerals: Indo-European *quetwor “four” (Latin quattuor, An. Ind. catvara, Slav. četyre, etc.) – Hung. kettő, Khanty kät, Mansi kit, Erzia kavto “two", Komi kvajt, Udm kuat ', Khanty kut, Erzya kota, etc. "six"; PIE *seks “six" (Latin sex, Ger sechs, Slav. šestĭ, lit. šeši, etc.) – Turkic. sekiz “eight”, Hebrew šeš ”six”; Hebrew arba “six" – Georgian rva “eight” – Telugu aaru “six”. However, the most expressive is the likeness of Finno-Ugric and the Dravidian word for the number four: Fin. neljä, Erzia nile, Mansi nila, etc. – Malayalam nālu, Telugu naalugu, Tulu nāl etc.
4. Indo-European *deќm "ten" (Slav. desętĭ, O.Ind dáśa, lat. decem, etc.) corresponds to Udm., Komi das, hung. tiz „ten".
5. Neighboring numerals often rhyme: Russ sem’ „seven“ – vosem’ „eight“, dieviat’ „nine“ – desiat’ „ten“, Ger zwei "two" – drei "thre", Arm. yot' „seven“ – ut' „eight“, Türk. sekiz „nine“ – toquz „ten“, Fin. kahdeksan „eight“ – yhdeksän „nine“, Veps kahesa „eight“ – ühesa „nine“, Gondi sārūng “six’- ērūng “seven” etc. This phenomenon may have the following explanation:
An approximate quantity in the compare languages can be denoted by two adjacent or close numerals in a series of natural numbers (STEPANOVA A.V. 2007: 4).
6. Some facts talk about replacing old items with newer ones. For example, the Chuvash pillĕk ”five” corresponds in the other Turkic languages bileg, bilezik ”carpus, wrist” which at first could also mean "five". However, at some time in all Turkic languages, Chuvash except, a new word beš spread for referring to five. Another example is the replacement in the East Slavic languages of the Old Slavic četyredesętĭ "forty" by the word "sorok", borrowed from Proto-Chuvashes (Chuv. khǝрǝkh “forty”).
The remaining cases of similarities will be considered during further discussion. We begin our analysis by considering the origin of the name of a single object. Herewith, we will bear in mind that the thinking of primitive man proceeded by their laws, different from our formal-logical thinking. Before man came to the abstract understanding of numbers, the quantitative relationships between objects were joined with the objects themselves. They could be used in a variety of accounts for different categories of subjects. For example, while exchange equating the two rams to one cow confused the difference between the numbers one and two.
As one can see from the table, the words, used for the number one in the languages of considered family derive from different roots, except that the Old Indian éka can be likened to the Finno-Ugric words having the root *ek/ik. After further searches, similar numbers were found in several Iranian languages, in particular, Farsi – jak, Kurdish – ēk, and Gilaki – jek “one”. Words of Finno-Ugric languages (Komi, Udm kyk) meaning “two” derived from the same root by reduplication (ik-ik). Number two was seen initially as a couple, a sort of unit of the pair of objects – two eyes, ears, hands. The emergence of the dual grammatical number would be meaningless if the two pairs of items were not opposed to the large set of items, which had a separate category of number.
Taking into account the possible similarities in the names of neighboring numbers and the initially unconscious quantitative difference between the numbers 1 and 2, we assume that the Turk ikki “two” has the same origin and look for the original word which according its meaning could suit for the start of counting. After a short search, we can stop at the Indo-European pronoun *eĝ "I". We observe the same thing in Caucasian languages: Kab. sǝ „I“ – zi „one“, Chech. so „I“ – cha „one“, Rut. zi „I“ – sa „one“, Bud. zin „I“ – sǝ-b „on“, Ud. zu „I“ – sa „one“, Khin. zi „I“ – sa „one“ etc. It is quite logical for humans to begin counting from themselves, therefore, the same word might well be used to characterize myself and the number 1. Analysis of the symbolic meanings of numbers in the folklore led ethnographers to the conclusion that the symbolism of the one claimed the symbolism of the center too, and the number 1 came to mean the "divine" or "royal" number and a person that it defines (NOVIKOVA М.О. 1993, 278). The primitive man looked at the world from self-serving positions, which led him to identify himself with the unit, symbolizing the center.
The assumption that the primary identity of the numeral "one" and the pronoun "I" is also supported by the fact that other Indo-European word *sem meaning "one" corresponds to the pronoun “myself” in the Slavic languages. Derived words from this root in some Indo-European languages kept the sense "one" or mean "same", "equal", "similar" (Latin similis, Eng same, etc.) This numeral is the most ancient in the human language, as similar words meaning "one" can be found in many languages, in particular, in Daghestan (Andi, Godoberi, Tabasaran – seb, sab), Korean hana, Ainu šine etc.
Further confirmation of the identity of the numeral "one" and the pronoun "I" is the fact that some Indo-European words having meaning “one” (Latin ūnus, Gr οινοσ, Goth ains, Eng one, Old-Irish oen) are similar to the words meaning "I" in the Semitic languages (Hebrew, ani, Ar ana) and in Hungarian èn. The similarity of the first-person pronoun singular and the numeral "one" can be observed in Kabardian: se “I” – zy “one", Ingush: so «I», sa «my» – caI «one" (besides saI “man"). If the pronouns were used for counting, there should exist examples of using the second-person pronouns for accounting. At least one such example is present – PIE *dvou ”two" in sounding is like the PIE *tu “you” (singular). It would be logical to assume that the third-person pronoun was used with the meaning "three", but such a match is not found. There is an explanation for this:
At an early stage of the development of society, the concept of duality was the first step toward understanding quantity and plurality. Dual forms were used when talking about pairing (two persons, two objects), related actions, and states (KOBYAKOVA I.K., SHVACHKO S.A. 2017: 105).
This explains why the initial count was only up to two, followed by the uncertainty of "many". A distant echo of ancient human ideas about quantity was the practice of teaching children to count in elementary schools until recently. First, they were taught to distinguish between one object, two objects, and many objects. Thus, we can assume that using third-person pronouns to refer to three items was not necessary at the time of the birth of the count. Nevertheless, its tracks are found in the names of numbers. Indo-European and Dravidian words meaning "one" (Latin ūnus etc. – Tulu onji, etc., see above) correspond to the Indo-European words meaning "he, that, this" (Russian on, Lit. añs, Old Ind anyas, N Germ enn, Hittite anni). Interestingly, similar words in Semitic languages belong to the first person pronoun, just as Hung. én “I” does. This is because the same word for the speaker means "I", and for the listener – "he".
Overcoming uncertainty "a lot" happened by dividing a large number of subjects in pairs and further counting occurred already by pairs, and this explains the similarity of even numbers can be observed even within the same language: Hebrew šnaim «two» – šmone “eight", Hung. négy (in other Finno-Ugric neljä, nyl, nila a.o.) – Hung nyolc “eight”, Mansi nila “four”- n'ololov “eight”. Pair counting also explains the similarity in the names of numbers "one" and "two", another example of which can be a match: Lat. par “equal”, paria “couple" – Chuv pěr “one" (in other Turkic – bir). It is possible that the word came to the ancient Italics from the Proto-Chuvash.
Of course, while paired counting, the first two pairs were very clearly aware, therefore the number 4 became of particular importance. It was the last "small" number, after which large numbers followed, and all numbers from 1 to 4 acquired a special meaning in human consciousness, which is evidenced, for example, by all genres of Ukrainian folklore: riddles, proverbs, beliefs, etc (NOVIKOVA M.O. 1993: 276) while the number "five" is practically never found in folklore. The special significance of the number 4 is confirmed by the Indo-European *octou “eight" in the form of a dual number i. e. means two fours which is confirmed also by Aw. ašti "measure of length in four fingers".
In addition, one can note the aforementioned striking similarity between the Finno-Ugric and Dravidian words meaning “four”, while the names of the remaining numbers are completely different. The probability of a random coincidence is negligible; the indicated similarity is explained by the fact that the areas of formation of the Proto-Finno-Ugric and Proto-Dravidian languages were neighboring in their common Nostratic homeland. Strangely, the Corresponding Member of the Russian Academy of Sciences does not understand this and, citing this correspondence, in the same work states that “there are no parallels to the Finno-Ugric and Samoyedic numerals on the Nostratic and Eurasian background” (NAPOLSKIKH V.V. 2015: 290, 295). The existing language contact between the speakers of the PF-U and PDrav languages was interrupted approximately in the 6th millennium BC. This suggests that the number 4 was very ancient and was used in other Nostratic languages, although under different names. It corresponds to the directions of natural human spatial orientation (left-right, front-back) and, most importantly, to the number of fingers on one hand without the thumb, so the binary counting system easily transitioned to the quaternary one. At the same time, confusion could arise in the names of the number of pairs, since the uncertainty of “many” made itself felt for a long time, and a common name for the number “four” obviously did not exist.
When counting in pairs, the numerals 1 and 2 could easily become synonyms, which we observe in the similarity of the Turkic and Finno-Ugric numerals of this meaning. In connection with this assumption, the Indo-European *kʷetu̯er "four" can mean "two pairs", coming from the addition of two synonyms *(i)ki and *dvou. This Indo-European word is similar to the possible proto-form *tovärt "four" of the Turkic languages, which is considered in the etymologization of this numeral. From such a proto-form, both Chuv. tävatä and the widespread Turk. тört/dört "four" can be developed (SEVORTYAN E.V. 1980, 285). Metathesis and interruption of the stop consonants k and t are allowed (cf. Gr. τέτταρες "four", English quart "quarter"), therefore both forms may have a common origin, taking into account the proximity of the Proto-Indo-Europeans and Proto-Turks in the ancestral homeland.
Intertribal trade assisted in confusion when the names of numbers were no longer aligned with the pronouns of an unknown language for one of the contractors, but took a specific value of a number. Besides, due to the local character of trade relations, local countable nomenclature took place, and the standardization of number names did not occur for a long time. In such circumstances, it is possible that similar words were used for different numbers (Tulu enma "eight", Gondi anma "nine "), and different words for the same number were used as it is confirmed by the examples of even more recent times ("two" and "pair", "twelve" and "a dozen").
It is also logical to assume that odd numbers were not initially perceived in paired counting and appeared later. It is not without reason that they are considered “bad” numbers (in Slavic languages, the word likhoy means both “bad” and “odd”). This is explained by the fact that any oddness, “excess”, the world archaism tends to identify with an unordered, unstable-dynamic, and therefore dangerous, “bad” beginning (NOVIKOVA M.O. 1993: 278). Therefore, the similarity of odd numbers in Nostratic languages is expressed very vaguely and may simply be accidental or be the result of later borrowings.
However, despite some confusion in the names of even numbers less than ten, ten items have already been determined more or less clearly, helped by the number of fingers on both hands. This happened at a time when the northern Nostratic tribes migrated to Eastern Europe, as the languages of their descendants have nothing in common with Semitic-Hamitic, Kartvelian, and Dravidian names for the ten subjects. But Hebrew and Arabic words teša/tis`ah “nine” are somewhat like this numeral in some modern Indo-European languages. Is it a random coincidence or whether this phenomenon have some explanation, yet to be determined? Some Dravidian languages (Kurukh, Malto, Peng, Kui, Kuvi) have the form das for the number ten, close to the word of Indo-European languages, but they can be later borrowed from Hindi, Bengali, and other Indian languages, as the most widened Dravidian languages Telugu, Tamil, Tulu have nothing like. The rate of development of counting systems was very slow. People have learned to count after ten quite late, and the formation of the numerals went different ways for people, even speaking closely related languages. For example, the duodecimal system of accounts among the Germans said that the account after ten began after the split of the Indo-European community (III millennium BC). The advantage of the duodecimal system was the fact that 12 is divisible by two, three, and four, while 10 could be divided only by two and five (HIRT HERMAN. 1940). However, this advantage is not used by all peoples of the word.
The common Indo-European proto-form for the numeral "ten" is restored as *deќm, *dek̂m̥-t (Lat. děcěm, Germ. tehun, Slav. desętĭ, Lett. desmit, etc.). It is assumed that this is a compound word, the first part of which goes back to the PIE *du̯ei "two". Then the second part should have the meaning "five" and can be associated with Old German. *handu (Gothic handu, Old English hand) "hand", the origin of which is controversial (POKORNY J. 1949-1959: 191-192; VASMER MAX, 1964: 507-508; KlUGE FRIEDRICH, SEEBOLD ELMAR. 1989: 290). A very dubious interpretation, the Romans, who stood at a higher cultural level, could not borrow such a word from the Germans, and before that, there could be no contact between them. This numeral can be associated with Old Turk. *dekim "many", restored by the word tekim "many, multitude" recorded in monuments of ancient Turkic writing (NADELYAEV V.M. et al. 1969). It has a counterpart in modern Turkish takım "group, team". However, I did not find an explanation for the origin of this word. The Turks could use it in a general sense, while among the Indo-Europeans the similar had a more specific meaning. This could well have happened, which is confirmed by an example from the Tatar language, in which tugyz means both "nine" and "many". It can be assumed that the word is of Indo-European origin, but an explanation for its second part has yet to be found. Judging by the similarity of Latin děcěm, and Old Turkic *dekim, you need to look for a word in the form kim/kem and in the meaning of "five fingers", "hand".
It is more difficult with the number 10 in the Finno-Ugric languages, where different words are used for it. However, the most widespread primordial form can be restored as *deksan presented as a partial word in the Finnish numerals "eight" (kahdeksan) and “nine” (yhdeksän). These numbers, as well as in other Finno-Ugric languages, are formed by a form of "ten minus two” (kah has the same origin as kaksi “two") and ten without one (yh as yksi “one”). This assumption is known thinking that the Finnish word is supposedly borrowed from some Indo-European language. It is considered unacceptable and is disputed for other reasons. Instead, it is proposed that the second part of the Finnish words be considered not -deksan, but -eksan out of Fin. eksy "to be lost". Then "eight" should mean "without missing two" (out of ten), and "nine" – "without missing one" (HÄKKINEN KAISA. 2007: 315-316). However, FU *deksan, IE *deќm, as Old Turkic tekim, can be a common Nostratic heritage. The form *deksan was something simplified in other Finno-Ugric languages (Upper-Mari – dakšy, Low-Mari – daše, Vepsian – esa, Erzya and Moksha – ksa/kse). The simplified form das means ten in the Komi and Udmurt languages, but it is a loan word from Iranian, where similar words are also ten. The numerals eight and nine in the Komi and Udmurt languages contain the formant mys but its meaning remains unknown. When this question becomes clearer, then it will be possible to speak more confidently about the origin of the numerals "eight" and "nine" in the Finno-Ugric languages.
Another variant of the numeral "ten" is spread in the Baltic-Finnish and Mordvin languages: Finnish. kymmenen, Est. kümme, Erzya kemen 'etc. It is based on the name of the palm (Finnish kämmen, Est. kämmal, Veps. kämen', Khant. kömõn). The languages Mari, Mansi, and Sami have for "ten" the words lu, lov, love, logi, Hungarian has tíz. It is believed that they are based on the ancient Finno-Ugric word presented in Fin. lukea "to read" (HÄKKINEN KAISA. 2007: 532).
Since an odd number of objects was not perceived by people for a long time, the "extra" item was joined to a greater or lesser number. However, it is rightly to assume that the number 3 appeared earlier than other odd numbers and the relevant words could originate from the nearest even number 4 (as opposed to two, four subjects could be perceived sooner as three). Therefore, we consider forms of the numerals "three" and "four" in the Nostratic languages. We can see that Indo-European *treis “three”, Turkic tort “four "and Semitic-Hamitic *talat “three” (Class. Ar. rhalatah, Syrian-Ar. tlāte, Hebrew šaloš, etc.) have remote similarity. This led to assume their common origin from the word meaning "wrong, bad." Traces of it have been preserved in many Turkic languages as ters "wrong, perverse, complex, reverse, opposite”. Such traces are less distinct in Indo-European languages but still visible: lat. trīstus "bad," Old Eng. dryslic “awful”. Following the same way, we can take to examination of the Fin. kummalinen, Est. kummaline “strange” and others similar ones for the number 3 (Finnish kolme, Erzya kolmo). While metathesis of consonants, such words might mean "three", but similar words have not been found yet in other Finno-Ugric languages. If this assumption about the origin of the numeral 3 is true, then the Tur tört "four" should be a secondary name, produced from the names of three, as four originally was not a "bad" number. This change seems unlikely because of the special values of the number 4; however may have an explanation. In the early stage of the development of accounts, the number 3, because of its “incorrectness”, seemed to be incomprehensible to man and became a mystical connotation following the three coordinates of the universe by vertically (the upper, middle, and lower worlds). Since the number 4 is consistent with the coordinates in the horizontal plane, both numbers have equally great importance in human psychology. Such a phenomenon is reflected, for example, in the form of religious buildings – churches in Ukraine have long been "built with four angles and three tops". Another example could be a characteristic alternation of "three or four" in the Ukrainian archaic poetics: "Poles came by three ways, and the Tatars by four ones did” and many others (Popovich M.V. 1985: 82).
It is difficult to judge the origin of the numeral meaning "five". On the one hand, it could be likened to the nearest even numbers, and on the other hand, the name of the hand could be taken as corresponding to five fingers. The connection between the Russian piast', "handful", the numeral piat' "five", and English fist, was assumed by many researchers, but they proceeded from the fact that the name of the hand came from the numeral, and not vice versa. This is a topic for specialists. Be that as it may, five objects could become a unit of counting and, accordingly, the names "one" and "five" could become similar, as we see when comparing the Komi öti "one" and the Hungarian öt "five", which also has parallels in other Finno-Ugric languages. Further development of the meaning of this root word led to Proto-Saam. wüt "ten". Napol'skikh considers the numbers 'five' and 'ten' to be 'basic' and suggests Old Japanese itu and Old Korean utu 'five' should be included among them. He also attributes the numerals 'one hundred' and 'one thousand' to the basic numbers in the decimal system (NAPOLSKIKH V.V. 2015: 296-7). All these basic numbers should ascend to the basic number 'one'. In this case, the supposed proto-form of the basic numerals should have a quantitative and abstract meaning. Following the divine attitude of people to the unit, one must seek a sacred meaning in this proto-form, and its phonetics determines the direction of this search. Thus, we come to an understanding of the origin of the Proto-Slavic numeral edьnъ “one” and the name of the Germanic god Wodan, which do not have a satisfactory etymology. Something similar must exist in other languages.
It is even more difficult to judge the origin of the numerals meaning "seven" and "nine". The ways of their formation are different in different languages, but it is obvious that the number "nine" received its name later than "seven". With counting to eight and a good representation of all the previous numbers, seven should have had its name. Numbers greater than eight either received the meaning "many" or were combined into pairs, i.e., both "nine" and "ten" could be designated by one word. However, over time, "nine" also received its name, and in Indo-European languages it meant "new", judging by the fact that in these languages the words "new" and "nine" are similar. Nevertheless, this hypothesis is questionable:
It seems to me that the arguments in favor of the connection between the meanings of "nine" and "new" are not strong enough to consider the hypothesis that "nine" openly marked the inclusion of a new category of numerals proven; even less justified is the assumption that Proto-Indo-European at some point in its prehistory had a quaternary system. Using the example of Osset. farast "nine" literally "behind eight" Abaev shows that "eight" was a round number, at least in the eyes of the Ossetians, but he adds rather cautiously: "just like "ten"," which does not allow the Ossetian form to be mentioned as an argument in favor of the quaternary hypothesis. (VINTER V. 1989: 34)
V. Vinter looks at the problem very narrowly, practically not going beyond the Indo-European languages, but obvious parallels in the formation of numerals in different language families confirm the existence of the quaternary system. Therefore, this hypothesis remains a working one for us.
A certain connection between numerals and pronouns has already attracted the attention of linguists. For example, there is an opinion that the numeral two is used in many languages of the world to form the personal pronoun of the dual number "we two", "you two" (BABAYEV K.V.. 2009: 132-134). In principle, such a transformation is logical, provided that the numeral "two" occurred before the pronoun. However, it is believed that pronouns were initially absent from languages and developed from other lexical or morphological units of language (Ibid: 119), that is, they could also develop from numerals. Although in certain cases, the reverse process could also take place.
I look for the book of László Honti "Die Grundzahlwörter der uralischen Sprachen"